Chapter 3. Gaussian Filter

* 이 글은 Sebastian Thrun의 책 <Probabilistic Robotics>의 번역본 <확률론적 로보틱스>를 기반으로 작성했습니다.

* 아직 공부를 하고 있는 비전문가이기 때문에 잘못 이해하였거나 잘못 번역한 부분이 있을 수 있습니다. 해당 부분이 있다면 댓글 부탁드립니다.

 

Gaussian

다변량 정규 분포(multivariate normal distribution)로 빌리프(belief)를 표현하는 것

다변량 정규 분포 식 평균 &mu;, 공분산 &Sigma;

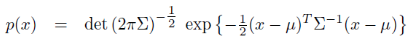
이때 평균 μ는 state x와 동일한 차원의 벡터로 표현되고, 공분산 Σ는 state x의 제곱의 차원과 같은 2차원 대칭 행렬이다.

 

Kalman filter

다음의 세 가지 속성이 있는 경우, 사후확률은 가우시안(Gaussian)이다.

• state의 전이 확률 p( x_t | u_t, x_t-1 ) 은 가우시안 노이즈 입력 인자를 갖는 선형 함수(linear function)이다.

이때 A_t는 n x n 행렬로 n은 state vector x_t의 차원과 같고, B_t는 n x m 행렬로 m은 control vector u_t의 차원과 같다.

확률변수 ε_t는 gaussian random vector로 state vector와 동일한 차원을 가지며, 평균 0, 공분산 R_t를 갖는다.

이를 통해 state의 전이 확률은 아래와 같이 평균을 A_tx_t-1 + B_tu_t, 공분산을 R_t로 하는 다변량 정규분포로 정의할 수 있다.

• 측정 확률 p( z_t | x_t )는 입력인자와 가우시안 노이즈에 따라 선형 함수의 형태이다.

measurement vector z_t의 차원이 k라고 할 때, C_t는 k x n의 행렬이고, δ_t는 평균이 0, 공분산 Q_t인 측정 노이즈이다.

초기 빌리프 bel(x_0)는 반드시 정규분포를 가져야 한다.

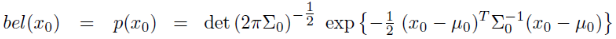
여기서 bel(x_t)는 시간 t에 대해 평균 μ_t, 공분산 Σ_t를 갖는다.

kalman filter의 입력으로 시간 t-1일 때의 belief는 평균 μ_t-1, 공분산 Σ_t-1로 표현되고, 이 값들을 업데이트 하기 위해 control u_t, measurement z_t가 필요하다.

2, 3행에서 ￣μ, ￣Σ 는 ￣bel(x_t)를 나타내고, 이는 z_t를 합치기 전의 값이 된다.

4, 5, 6행에서는 ￣bel(x_t)에 measurement z_t를 합쳐 bel(x_t)로 변형된다. 여기서 K_t는 칼만 이득(kalman gain)을 의미한다.

 

Extended Kalman Filter(EKF)

Kalman Filter(KF)와 마찬가지로 평균이 0인 가우시안 분포로 가정한다.

KF와의 차이점은 motion model과 observation model을 선형으로 가정하지 않고 비선형 함수로 확장한 것이다(거의 대부분의 실제 시스템은 비선형).

EKF는 기존 KF의 선형 모델을 비선형 함수인 g(u_t,x_t-1)와 h(x_t)로 바꿈으로써 비선형으로 확장한 모델

하지만 이 과정에서 아래와 같은 문제가 발생한다.

입력은 가우시안 분포이지만 시스템의 비선형성에 의해 출력은 가우시안 분포가 아니다. 이러한 문제를 해결하기 위해 비선형함수를 선형화(Linearization)하는 과정이 필요하다.

EKF에서 비선형 함수를 선형화하기 위해 1차 테일러 근사(first order Talyor Expansion)를 사용한다.

• Motion Model

• Observation Model

이때 비선형 함수들을 state로 편미분하여 matrix를 생성하는데, 이 matrix를 Jacobian이라고 부르며, 두 matrix는 아래와 같이 표기한다.

Jacobian matrix

• Jacobian matrix는 non-square matrix
• 비선형 함수 vector가 g(x)일 때, Jacobian G_x는 다음과 같이 계산된다.

이러한 Jacobian은 매순간 모든 변수에 대해 미분을 하여 선형화된 값을 얻어낸다.

 

위의 그림은 테일러 근사화를 통해 선형화 하였을 때를 보여준다.

위의 그림은 입력의 분산(variance)가 큰 경우를 보여주며, 아래 그림은 분산이 작은 경우를 보여준다. 분산이 큰 경우 실제 비선형 함수 출력의 평균값과 선형화를 통해 계산된 평균값의 차이가 큰 것을 알 수 있다. 반면 분산이 작은 경우는 두 값의 차이가 적다. 따라서 선형화를 할 때 분산이 클수록 실제 함수를 반영하지 못한다는 것을 알 수 있다.

선형화된 motion model과 observation model을 이용한 bayes filter는 다음과 같다.

• linearized prediction model

• linearized correction model

EKF의 알고리즘은 다음과 같다.

KF 알고리즘과 비교해 2, 5행에서 선형함수 대신 비선형 함수가 사용된 것과, 3, 4행에서 선형함수의 matrix가 Jacobian matrix로 수정되었다.

 

 

참고 사이트 : http://jinyongjeong.github.io/2017/02/14/lec03_kalman_filter_and_EKF/