* 이 글은 Sebastian Thrun의 책 <Probabilistic Robotics>의 번역본 <확률론적 로보틱스>를 기반으로 작성했습니다.
* 아직 공부를 하고 있는 비전문가이기 때문에 잘못 이해하였거나 잘못 번역한 부분이 있을 수 있습니다. 해당 부분이 있다면 댓글 부탁드립니다.
State Estimation이란 센서 데이터로부터 정량적인 추정값을 도출해내는 문제를 다루는 것이다.
이 책에서 다루는 대부분은 연속형 공간(continuous space)에서 무언가를 결정하고 추정하는 문제이기 때문에, 모든 연속형 확률 변수는 확률 밀도 함수(PDF, Probability Density Function)을 포함하고 있다. 대표적인 확률 밀도 함수로 1차원 정규 분포 함수(normal distribution, 평균은 μ, 분산은 σ2)가 있다. 정규분포의 확률 밀도 함수는 가우시안 함수(gaussian function)으로 정의할 수 있다.

만약 x가 스칼라(scalar)가 아닌 다차원 벡터(vector)라면, 다변량 정규 분포(multivariate normal distribution)이라 한다.

μ는 평균 벡터, Σ는 공분산 행렬(covariance matrix), 위 첨자 T는 벡터의 행과 열을 교환하는 전치 연산(Transpose)을 의미한다. p(x,y)는 X=x and Y=y 일 때의 확률을 의미하고, 두 확률 변수가 독립일 경우 결합 확률 분포는 p(x,y) = p(x) p(y) 이다.
확률 변수 Y가 y임을 이미 알고 있는 조건하에서 확률 변수 X가 x 값을 가질 확률은 p(x | y)로 조건부 확률(conditional probability)이라고 한다. 이때 p(y) > 0이면, 조건부 확률은 p(x | y) = p(x,y) / p(y)로 나타낼 수 있고, 확률 변수 X, Y가 독립이면 p(x | y) = p(x)p(y) / p(y) = p(x) 로 나타낼 수 있다.
state(xt)
state는 동적 스테이트(dynamic state)와 정적 스테이트(static state)로 나뉜다.
state에는 로봇 포즈(pose), 속도, 센서의 정상 작동 여부 등 로봇에 관한 변수가 포함된다.
- pose는 global coordinates를 기준으로 상대적 위치와 방향값으로 구성된다. 6-DoF의 경우 3개의 직교 좌표와 3개의 방향 좌표(roll, pitch, yaw)로 구성된다.
- 로봇 조작(manipulation)에서 pose는 로봇의 액추에이터 관련 환경설정 변수도 포함한다.(ex_ 로봇 팔의 회전 부분의 관절 각도)
- 로봇 속도는 일반적으로 dynamic state이다.
- 환경 내에 있는 주변 객체들의 위치 및 특징도 포함한다. 환경 내에서 뚜렷하고 고정된 feature인 landmark의 형태로 가정한다.
- 움직이는 물체와 사람의 위치, 속도 또한 잠재적인 state이다.
- 센서의 고장 여부, 배터리 충전 수준 등도 state 변수가 될 수 있다.
측정 데이터(environment measurement data)
-> by sensor
-> t에서의 측정을 z_t
제어 데이터(control data)
-> odometry
-> t에서의 측정을 u_t
p(x_t | x_{0:t-}1, z_{1:t-1}, u_{1:t})
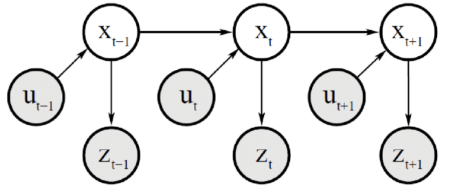
state x가 완전성을 만족하는 경우, x에는 이전 단계에서 발생한 모든 내용이 담겨있다. x_{t-1}은 이 시점까지의 모든 이전 단계의 제어 u_{1:t-1}과 측정 z_{1:t-1}의 유의미한 통계량이라 말할 수 있다. 우리가 state x_{t-1}을 알고 있다면, 제어 u_t만 생각하면 된다. 또한 p(z_t | x_{0:t}, z_{1:t-1}, u_{1:t})는 p(z_t | x_t)로 정리할 수 있다.
p(x_t | x_{0:t-1}, z_{1:t-1}, u_{1:t}) = p(x_t | x_{t-1}, u_t)
이때 u(odometry)를 먼저 구하고 z(measurement)를 취하는 것으로 가정한다.
state x_t는 x_{t-1}로부터 확률적으로 생성되기 때문에, x_t가 생성되는 확률 분포를 지정하는 것이 합리적이다.
belief

bel(x_t)는 사용 가능한 데이터(measurement, odometry)가 주어졌을 때 state에 대한 사후확률로 볼 수 있다.
bel(x_t)는 measurement를 반영한 후에 belief 결과를 얻는다. 하지만 때때로 measurement(z)를 반영하기 전에 사후확률을 계산하는 것이 더 효율적일 수도 있다. 이때 사후 확률은  ̄bel(x_t) = p(x_t | z_{1:t-1}, u_{1:t}) 로 표현할 수 있다.
 ̄bel(x_t)로부터 bel(x_t)를 계산하는 과정을 measurement update라고 한다.
베이즈 필터(Bayes Filter)

3행에서는 x_t-1과 u_t와 생성된 이전의 belief를 이용해 x_t의 belief를 계산 -> prediction
4행에서는 bel(x_t)에 z_t가 나타날 확률을 곱함 -> measurement update
마르코프 가정(Markov assumption)
현재 state x_t를 안다면, 과거와 미래의 데이터가 독립적이라고 가정
'Probabilistic Robotics' 카테고리의 다른 글
| Chapter 5. Robot Motion (0) | 2022.07.30 |
|---|---|
| Chapter 3. Gaussian Filter (0) | 2022.07.30 |
